I feel this should be viewed in the context of the Hutter prize and it is important to examine how this will affect AI. The program given simply compresses a series of integers, although thw program is eventually intended to provode for compression based on constructing a probability table.
The arrangement is in order of decreasing probability. Your first word in a string is simply the mean frequency of every word. The list for the second word is the probabilities BEARING IN MIND THAT THE FIRST WORD IS ******. I was assuming that the list was prepared using DCA. OK something else could be, my rationalizations like always feminine singular is the way I think. DCA if applied will bring out gender differences with eigenvctors containg la, el, los, las.
DCA of course talks the language of probability, it does not attempt to parse. It might implicity parse under certain circumstances, in all European languages, with the exception of English there is gender and agreement. DCA will pick this up and could be described as a partial parsing.
A diagram of what is happenning is given below.
Here is the guts of it There are a few algorithms in here which are not really relevant. You can compile it into whatever system you wish. There are some I/O routines which the user will have to write for himself. They are fairly trivial.
/* This program is designed to achieve the ultimate in compression. THere are codes like the Huffing code that lose very little
entropy. This provides for the ultimate. It is a well known mathematical fact that the number of ways of arranging objects in holes
is N!/(Pi(n(i)!(N-Sigman(i))!) This assumes that each site is occupied by 1 and 1 only object.
The problem then is to enumerate each individual configuration. If each configuration can be numbered compression has been achieved.
Consider N!/(n!(N-n)!) If we can evaluate that expression the complete expression can be evaluated. For we can work out the
configuration for n(0), We are now left with N-n(0) places. Then n(1), N-n(0) and so on. The algorithm used is the following:-
If we take the n[0]th poaition of number n[0] and place it somewhere we know that the number of arrangements of the remaining
n[0]-1 will be P!/((n[0]-1)!(P-1-n[0])!)
This gives us a scheme of numbering. If we calculate Sigma(P!/((n[0]-1)!(P-1-n[0])!)) as ball -> P position we have a numbering scheme.
*/
class Factorial{
/* This class is the class of factorials. arr starts off with 1,2,3.....n It is created in this form by Factorial(int).
divide divides by an integer. It does this by finding the Highest common factor using Euclid's algorithm, and divides
repeatedly until the number you are divising by becomes equal to 1. If division is by a factorial the numbers are taken
in turn. In this way we get N!/(n!(N-n)!) in is simplest form.
*/
public:
int n;//The number of numbers in the factorial
int *arr;
Factorial(int);//sets up factorial. Initially the numbers are sequential
void divide(Factorial);//This divides by another factorial. It does this to limit the size of the numbers.
void divide(int);//This divides by a single integer
};
class Big{
/* This is the Big integer class which ios the guts of the program.
n is the number of I*4 wordsin the integer
*arr is the array of numbers
We need to be able to perform the basic arithmetrical operations and in addition needs to have a remainder when dividing by a big
integer, Basically we use these remainders are the numbers of N!/(n!(N-n)!). To make division easier the big integer we are
dividing by is presented as a series of I84 integers. We divide by each in turn.
*/
public:
int n;
int *arr;
void add(int);//Add I*4 integer
void add(Big);//Add another
void sub(Big);//Subtract big integer
void mul(int);//Multiply by I*4 integer
void mul(Big);//Muliply by big integer. In normal form, not in the special form for division.
int div(int);//Divide by I*4 inter
Big div(Big);//Big integer division
Big(int);//create a big integer of length n
Big();//create a big integer without arrays
Big(int*,int);//Create a big integer from the form for division
Big(Factorial);//Convert a factorial into a big integer
void wr(CFile*);//Write big integer onto file
void rd(CFile*);//read big integer from file
int bits();
boolean operator<(Big a);//These are simply comparison operators boolean operator>(Big a);
};
class Compress{
/* This class contains the complete compressed information - sufficient for loss free compression.
*/
public:
int n,max;
// n is the number of differnt numbers in the string.
// max is the highest number in the string, not necessarily the same as the above.
int *fact,*trans;
// fact contains the number of numbers in each non zero category
// trans is a table for translating each number into its value.
Big *b;//The big integer
void ecode(int*,int);//Encode
void rd(CFile*);//read and write files
void wr(CFile*);
Compress();
int* dcode(int* n);//decode
};
class Entry{
public:
CString s;
int q;
unsigned int ind;
};
class HashArray{
public:
int size;
int last[3];
int places,nplaces;
int nvar;
int pos,posa,mvar;
int *len;
unsigned short **mat;
int **res;
void stats(int*);
int in;
int ksiz;
Entry *array;
int put(char*);
int get(char*);
boolean IsMatch(char*);
void Del(char *);
HashArray(int);
void rd(CFile*);
void wr(CFile*);
void sort(int*);
int init(int);
int combine();
void Vect(int*,int);
void del();
};
Big encode(int*,int,int);
void decode(Big,int*,int,int);
boolean IsLetter(unsigned char);
double Gosper(int);//This is a routine that gives the log of the factorial without actually evaluating it. It calculates entropy.
double kern(int);
void Diag(int*,int);
void Dev(double*,double*,int);
double *VecMat(int *vec);
int decomp(unsigned char*,int*,int);
int compr(int*,unsigned char*,int);
Factorial::Factorial(int m){//This constructs a factorial of size m
n=m;
arr=new int[n];
for(int i=0;i>1;
}
j=j+(n-i-1)*32;
return j;
}
return j;
}
Big::Big(Factorial f){//Create a big integer in divide form from a factorial
unsigned int *ar,q;
int mm=1+f.n/2;//Inconcievable resultant integer as big as this
ar=new unsigned int[mm];
n=0;
ar[n]=1;
for(int i=1;iWrite(&m,sizeof(int));
f->Write(arr+i,m*sizeof(int));
}
void Big::rd(CFile *f){//Read a big inter from file ff
f->Read(&n,sizeof(int));
arr=new int[n];
f->Read(arr,n*sizeof(int));
}
boolean Big::operator<(Big a){//These two functions allow us to use inequalities in the way they are used for ordinary unsigned // integers in C++ and Java for(int i=0;i(unsigned int)a.arr[i])return false;
}
return false;
}
boolean Big::operator>(Big a){
for(int i=0;i(unsigned int)a.arr[i])return true;
if((unsigned int)arr[i]<(unsigned int)a.arr[i])return false; } return false; } Compress::Compress(){//Creates an empty compress class n=0; } int *Compress::dcode(int *qq){ /* This subroutine decompresses a string. It does this by first looking for the positions of 1s then 2s etc. It decodes each individual string. *qq on exit contains the length of the string. */ int len=0; int *arr; int i,j,k,m; Big *mul;// Contains the big integers for multiplication for(i=0;imax)max=fact[i];//Get longest string
int *pos=new int[max];
for(i=n-1;i>0;i--){//Loop is in inverse order
Big d=b[0].div(mul[i-1]);//Divide. Remainder represents the configuration
int mm=fact[n-1-i];
decode(d,pos,mm,d.n);//Get string
k=m=0;
for(j=0;j=mm)break;//are we at end
}
k++;
}
delete d.arr;
delete mul[i-1].arr;
}
delete pos;
pos=new int[n];
zero(pos,n*sizeof(int));
i=0;
max=0;
while(i==0){//pos contains the translation table
m=trans[max++];
if(m<1)continue; i="1;" k="0;kRead(&max,sizeof(int));
f->Read(&n,sizeof(int));
fact=new int[n];
trans=new int[max+1];
f->Read(fact,n*sizeof(int));
f->Read(trans,(max+1)*sizeof(int));
b->rd(f);
}
void Compress::wr(CFile *f){//write class to file f
f->Write(&max,sizeof(int));
f->Write(&n,sizeof(int));
f->Write(fact,n*sizeof(int));
f->Write(trans,(max+1)*sizeof(int));
b->wr(f);
}
void Compress::ecode(int *str,int len){
/* This subroutine encodes a string of length len in *str. In order to facilitate decoding it takes the highest number first
*/
int i,j,k,m,nbits=0;
Big *mul,*val;
b=new Big[1];
max=0;
for(i=0;imax)max=str[i];
}
fact=new int[max];//Get numbers of each number in string
trans=new int[max+1];
n=0;
zero(fact,max*sizeof(int));
zero(trans,(max+1)*sizeof(int));
for(i=0;ib2)){//Compare. When the number of positions is greater than the big integer we have just passed position
b2.sub(b3);//Subtract b3
b3.mul(j-1);//Calculate number of permutations for the rest
b3.div(j-ma);
j++;
}
pos[npos-1-i]=j-2;
zero(b3.arr,dim*sizeof(int));
ma--;
}
delete b3.arr;
}
Big encode(int *pos,int npos,int dim){
/* This one encodes. It is the analogue of the one above.
*/
Big b2(dim);
Big b3(dim);
int ma=npos;
for(int i=0;ij)str[i]++;
}
millisec();
c.ecode(str,n);
arr[0]=millisec();
stra=c.dcode(&k);
arr[1]=millisec();
int_put(arr,2);
for(i=0;i0;i--){
j=f.arr[i];
if(j==1)continue;
m=q.div(j);
}
zero(q.arr,q.n*sizeof(int));
i=0;
k=nbins;
while(nbins>1){
q.mul(nbins);
j=ranmod(nbins);
q.add(j);
str[i++]=j;
for(int ii=0;iiif(bins[ii]==0)continue;
if(j==0){
j=ii;
break;
}
j--;
}
bins[j]--;
if(bins[j]==0)nbins--;
}
goto loop;
}
}
EUCLID'S ALGORITHM
int euclid_algorithm(int i,int j){//This algorithm impliments euclids algorithm for integers i and j
int k=1;
while(k!=0){
k=i%j;
i=j;
j=k;
}
return i;
}
bcopy (utility function)
/* This subroutine copies one string onto another.
len bytes are copied from x to y*/
void bcopy(void *x,void *y,int len){
int i=len/4;
int j,k;
_asm{
mov esi,x
mov edi,y
mov ecx,i
rep movsd
mov j,edi
mov k,esi
}
int *xx=(int*)x;
int *yy=(int*)y;
if((len&3)==0)return;
_asm{
mov edi,j
mov esi,k
xor eax,eax
mov ecx,len
and ecx,3
rep movsb
}
}
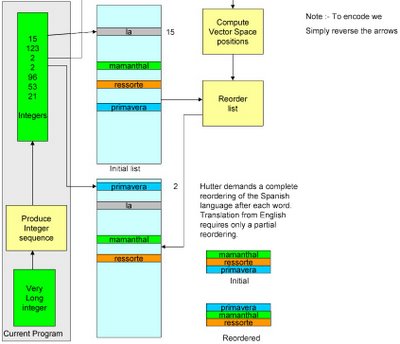
The arrangement is in order of decreasing probability. Your first word in a string is simply the mean frequency of every word. The list for the second word is the probabilities BEARING IN MIND THAT THE FIRST WORD IS ******. I was assuming that the list was prepared using DCA. OK something else could be, my rationalizations like always feminine singular is the way I think. DCA if applied will bring out gender differences with eigenvctors containg la, el, los, las.
DCA of course talks the language of probability, it does not attempt to parse. It might implicity parse under certain circumstances, in all European languages, with the exception of English there is gender and agreement. DCA will pick this up and could be described as a partial parsing.
A diagram of what is happenning is given below.

Here is the guts of it There are a few algorithms in here which are not really relevant. You can compile it into whatever system you wish. There are some I/O routines which the user will have to write for himself. They are fairly trivial.
/* This program is designed to achieve the ultimate in compression. THere are codes like the Huffing code that lose very little
entropy. This provides for the ultimate. It is a well known mathematical fact that the number of ways of arranging objects in holes
is N!/(Pi(n(i)!(N-Sigman(i))!) This assumes that each site is occupied by 1 and 1 only object.
The problem then is to enumerate each individual configuration. If each configuration can be numbered compression has been achieved.
Consider N!/(n!(N-n)!) If we can evaluate that expression the complete expression can be evaluated. For we can work out the
configuration for n(0), We are now left with N-n(0) places. Then n(1), N-n(0) and so on. The algorithm used is the following:-
If we take the n[0]th poaition of number n[0] and place it somewhere we know that the number of arrangements of the remaining
n[0]-1 will be P!/((n[0]-1)!(P-1-n[0])!)
This gives us a scheme of numbering. If we calculate Sigma(P!/((n[0]-1)!(P-1-n[0])!)) as ball -> P position we have a numbering scheme.
*/
class Factorial{
/* This class is the class of factorials. arr starts off with 1,2,3.....n It is created in this form by Factorial(int).
divide divides by an integer. It does this by finding the Highest common factor using Euclid's algorithm, and divides
repeatedly until the number you are divising by becomes equal to 1. If division is by a factorial the numbers are taken
in turn. In this way we get N!/(n!(N-n)!) in is simplest form.
*/
public:
int n;//The number of numbers in the factorial
int *arr;
Factorial(int);//sets up factorial. Initially the numbers are sequential
void divide(Factorial);//This divides by another factorial. It does this to limit the size of the numbers.
void divide(int);//This divides by a single integer
};
class Big{
/* This is the Big integer class which ios the guts of the program.
n is the number of I*4 wordsin the integer
*arr is the array of numbers
We need to be able to perform the basic arithmetrical operations and in addition needs to have a remainder when dividing by a big
integer, Basically we use these remainders are the numbers of N!/(n!(N-n)!). To make division easier the big integer we are
dividing by is presented as a series of I84 integers. We divide by each in turn.
*/
public:
int n;
int *arr;
void add(int);//Add I*4 integer
void add(Big);//Add another
void sub(Big);//Subtract big integer
void mul(int);//Multiply by I*4 integer
void mul(Big);//Muliply by big integer. In normal form, not in the special form for division.
int div(int);//Divide by I*4 inter
Big div(Big);//Big integer division
Big(int);//create a big integer of length n
Big();//create a big integer without arrays
Big(int*,int);//Create a big integer from the form for division
Big(Factorial);//Convert a factorial into a big integer
void wr(CFile*);//Write big integer onto file
void rd(CFile*);//read big integer from file
int bits();
boolean operator<(Big a);//These are simply comparison operators boolean operator>(Big a);
};
class Compress{
/* This class contains the complete compressed information - sufficient for loss free compression.
*/
public:
int n,max;
// n is the number of differnt numbers in the string.
// max is the highest number in the string, not necessarily the same as the above.
int *fact,*trans;
// fact contains the number of numbers in each non zero category
// trans is a table for translating each number into its value.
Big *b;//The big integer
void ecode(int*,int);//Encode
void rd(CFile*);//read and write files
void wr(CFile*);
Compress();
int* dcode(int* n);//decode
};
class Entry{
public:
CString s;
int q;
unsigned int ind;
};
class HashArray{
public:
int size;
int last[3];
int places,nplaces;
int nvar;
int pos,posa,mvar;
int *len;
unsigned short **mat;
int **res;
void stats(int*);
int in;
int ksiz;
Entry *array;
int put(char*);
int get(char*);
boolean IsMatch(char*);
void Del(char *);
HashArray(int);
void rd(CFile*);
void wr(CFile*);
void sort(int*);
int init(int);
int combine();
void Vect(int*,int);
void del();
};
Big encode(int*,int,int);
void decode(Big,int*,int,int);
boolean IsLetter(unsigned char);
double Gosper(int);//This is a routine that gives the log of the factorial without actually evaluating it. It calculates entropy.
double kern(int);
void Diag(int*,int);
void Dev(double*,double*,int);
double *VecMat(int *vec);
int decomp(unsigned char*,int*,int);
int compr(int*,unsigned char*,int);
Factorial::Factorial(int m){//This constructs a factorial of size m
n=m;
arr=new int[n];
for(int i=0;i
}
j=j+(n-i-1)*32;
return j;
}
return j;
}
Big::Big(Factorial f){//Create a big integer in divide form from a factorial
unsigned int *ar,q;
int mm=1+f.n/2;//Inconcievable resultant integer as big as this
ar=new unsigned int[mm];
n=0;
ar[n]=1;
for(int i=1;i
f->Write(arr+i,m*sizeof(int));
}
void Big::rd(CFile *f){//Read a big inter from file ff
f->Read(&n,sizeof(int));
arr=new int[n];
f->Read(arr,n*sizeof(int));
}
boolean Big::operator<(Big a){//These two functions allow us to use inequalities in the way they are used for ordinary unsigned // integers in C++ and Java for(int i=0;i
}
return false;
}
boolean Big::operator>(Big a){
for(int i=0;i
if((unsigned int)arr[i]<(unsigned int)a.arr[i])return false; } return false; } Compress::Compress(){//Creates an empty compress class n=0; } int *Compress::dcode(int *qq){ /* This subroutine decompresses a string. It does this by first looking for the positions of 1s then 2s etc. It decodes each individual string. *qq on exit contains the length of the string. */ int len=0; int *arr; int i,j,k,m; Big *mul;// Contains the big integers for multiplication for(i=0;i
int *pos=new int[max];
for(i=n-1;i>0;i--){//Loop is in inverse order
Big d=b[0].div(mul[i-1]);//Divide. Remainder represents the configuration
int mm=fact[n-1-i];
decode(d,pos,mm,d.n);//Get string
k=m=0;
for(j=0;j
}
k++;
}
delete d.arr;
delete mul[i-1].arr;
}
delete pos;
pos=new int[n];
zero(pos,n*sizeof(int));
i=0;
max=0;
while(i==0){//pos contains the translation table
m=trans[max++];
if(m<1)continue; i="1;" k="0;k
f->Read(&n,sizeof(int));
fact=new int[n];
trans=new int[max+1];
f->Read(fact,n*sizeof(int));
f->Read(trans,(max+1)*sizeof(int));
b->rd(f);
}
void Compress::wr(CFile *f){//write class to file f
f->Write(&max,sizeof(int));
f->Write(&n,sizeof(int));
f->Write(fact,n*sizeof(int));
f->Write(trans,(max+1)*sizeof(int));
b->wr(f);
}
void Compress::ecode(int *str,int len){
/* This subroutine encodes a string of length len in *str. In order to facilitate decoding it takes the highest number first
*/
int i,j,k,m,nbits=0;
Big *mul,*val;
b=new Big[1];
max=0;
for(i=0;i
}
fact=new int[max];//Get numbers of each number in string
trans=new int[max+1];
n=0;
zero(fact,max*sizeof(int));
zero(trans,(max+1)*sizeof(int));
for(i=0;i
b2.sub(b3);//Subtract b3
b3.mul(j-1);//Calculate number of permutations for the rest
b3.div(j-ma);
j++;
}
pos[npos-1-i]=j-2;
zero(b3.arr,dim*sizeof(int));
ma--;
}
delete b3.arr;
}
Big encode(int *pos,int npos,int dim){
/* This one encodes. It is the analogue of the one above.
*/
Big b2(dim);
Big b3(dim);
int ma=npos;
for(int i=0;i
}
millisec();
c.ecode(str,n);
arr[0]=millisec();
stra=c.dcode(&k);
arr[1]=millisec();
int_put(arr,2);
for(i=0;i
j=f.arr[i];
if(j==1)continue;
m=q.div(j);
}
zero(q.arr,q.n*sizeof(int));
i=0;
k=nbins;
while(nbins>1){
q.mul(nbins);
j=ranmod(nbins);
q.add(j);
str[i++]=j;
for(int ii=0;ii
if(j==0){
j=ii;
break;
}
j--;
}
bins[j]--;
if(bins[j]==0)nbins--;
}
goto loop;
}
}
EUCLID'S ALGORITHM
int euclid_algorithm(int i,int j){//This algorithm impliments euclids algorithm for integers i and j
int k=1;
while(k!=0){
k=i%j;
i=j;
j=k;
}
return i;
}
bcopy (utility function)
/* This subroutine copies one string onto another.
len bytes are copied from x to y*/
void bcopy(void *x,void *y,int len){
int i=len/4;
int j,k;
_asm{
mov esi,x
mov edi,y
mov ecx,i
rep movsd
mov j,edi
mov k,esi
}
int *xx=(int*)x;
int *yy=(int*)y;
if((len&3)==0)return;
_asm{
mov edi,j
mov esi,k
xor eax,eax
mov ecx,len
and ecx,3
rep movsb
}
}


2 Comments:
You said:
The problem then is to enumerate each individual configuration. If each configuration can be numbered compression has been achieved.
How do you figure that? Even if true, that does not mean that they represent minimum loss-free compressions. There is something missing here. (I don't completely understand the formulas but I get the idea. I would like to start with an informal explanation if possible)
Jim Bromer
It represents the maximum loss free compression provided that there is no relationship between the words. Further compression can be made iff such a relationship extis.
It is important to understand this iff thouroughly. You get about 20MB for the Hutter corpus if you assume no relationship between the words. The best compression so far is 17MB. This is achieved using fragment compression. Now there is a relationship between a word's meaning and its syllabic structure. Most students of a language readily appeciate this but the Hutter prize has proved this in quite a rigorous way.
It is also true to say that an AI technique based on word frequency must be capable of compressing to 17MB or less. This is because we can get from an integral representation to a syllabic representation be means of a matrix multiplication.
As M1*M2 = M3 this resolves itself down to a matrix. A product matrix (suppose M2 is the identity matrix)must compress at least as much.
Post a Comment
<< Home